本文共 2686 字,大约阅读时间需要 8 分钟。
适读人群:Java 初级
学习笔记
基础概念
线程是无处不在的
先说说几个基本的概念吧
一个进程中可以包含多个线程,同一个进程中的线程共享该进程所申请到的资源,如内存空间和文件句柄等
从JVM的角度来看,线程是进程中的一个组件(Component)
Java程序中任何一段代码总是执行在某个确定的线程中
Java中线程分为守护线程(Daemon Thread)和用户线程(User Thread)
用户线程:JVM正常停止前应用程序中的所有用户线程必须先停止完毕,否则JVM无法停止
守护线程:不会影响JVM的正常停止,通常执行一些重要性不高的任务,如监视其他线程的运行情况
在多线程的运行中,我们需要注意每个段代码是由哪一个线程去负责执行的,这关系到性能问题、线程安全
System.out.println("The ** method was executed by thread: " + Thread.currentThread().getName()); 如上可以看看对应方法是哪个线程负责执行的,当然你可以创新一个新的线程,并由新的线程负责,来验证你的猜想

创建并运行
在Java中,一个线程就是一个java.lang.Thread的实例
创建一个Thread类,JVM会为这个线程实例分配两个调用栈(Call Stack)所需的内容空间
两个调用栈,一个用于跟踪Java代码间的调用关系,另一个用于跟踪Java代码对本地代码(即Native代码)的调用关系
假设我们在main方法中创建了一个新的线程,那么新的thread就是main线程的子线程,它们也就是父子线程关系
在默认情况下父线程为守护线程,则子线程也同样为守护,用户线程也是如此,当然你也可以通过setDaemon方法来修改这一属性
状态与上下文切换
人这一生有很多种状态,线程也是一样的
我们可以通过getState方法获取,返回值是Enum(枚举)
| 状态 | 备注 |
|---|---|
| NEW | 有且仅有一次处于此状态,刚创建而未启动的线程 |
| RUNNABLE | 复合状态,包括READY和RUNNING,当READY被JVM线程调度器调度则进入RUNNING状态,RUNNING表示线程正在执行,即run方法代码正在由cpu执行,当实例yield方法被调用或者线程调度器原因,RUNNING也会转为READY |
| BLOCKED | 线程发起I/O操作后或试图去获取其他线程的持有锁,则进入这个状态,这个状态不会占用CPU资源,以上操作后转为RUNNABLE状态 |
| WAITING | 执行某些方法(Object.wait()、Thread.join()、LockSupport.park())处于无限等待其他线程执行特定操作的状态,某些方法(Object.notify()、Object.notifyAll()、LockSupport.unpark(thread)让线程从WAITING转换为RUNNABLE |
| TIMED_WAITING | 处于有时间限制的等待其他线程执行特定操作,如果其他线程没有执行,时间到了,就自动转为RUNNABLE |
| TERMINATED | 执行结束的线程,也是仅有一次的状态,无论成功或异常 |
而一个线程从RUNNABLE转换为BLOCKED、WAITING、TIMED_WAITING几个状态的过程就意味着上下文切换(Context Switch)
上下文信息:包括CPU的寄存器和程序计数器在某一时间点的内容等
就好像你在和父母打电话的时候,突然你女朋友打了进来,你果断接了女朋友的约会邀请,然后又重新接上父母这边的并续上刚刚的聊天内容
从RUNNABLE转到其他,上下文信息(聊天内容)需要先存储起来,然后再重新进入RUNABLE状态时,回复之前保存的线程的上下文信息(聊天内容),在保存和回复的过程就是上下文切换
在保存或恢复就是需要开销的,如CPU时间开销和CPU缓存内容失效等
你可以看看自己的Java程序运行时的上下文切换情况,我这边是win7,所以用了windows自带的perfmon
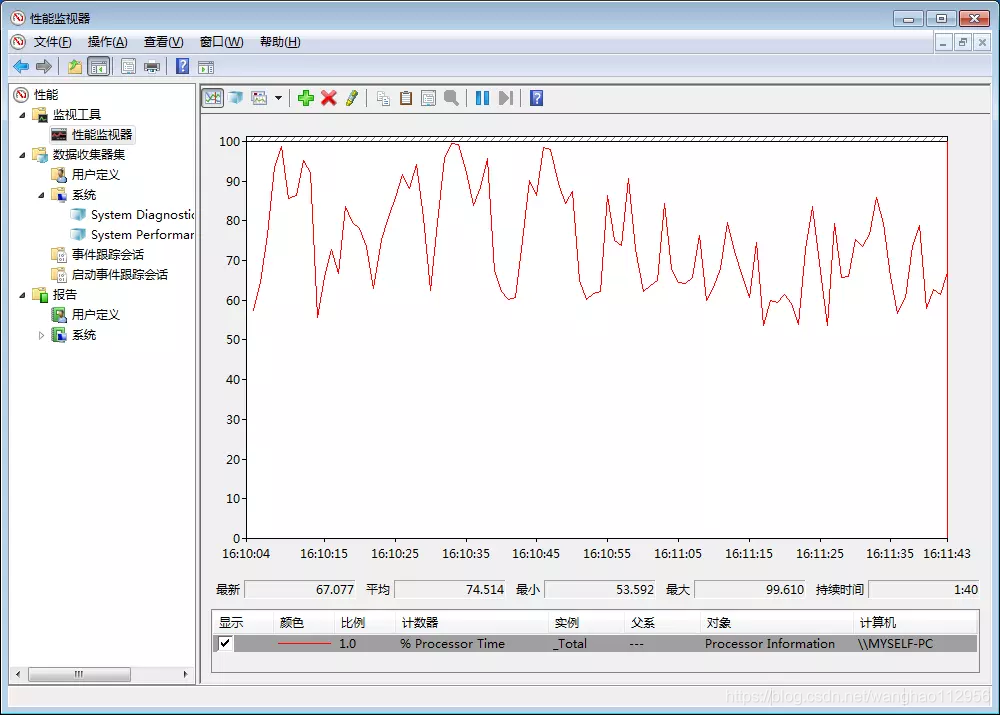
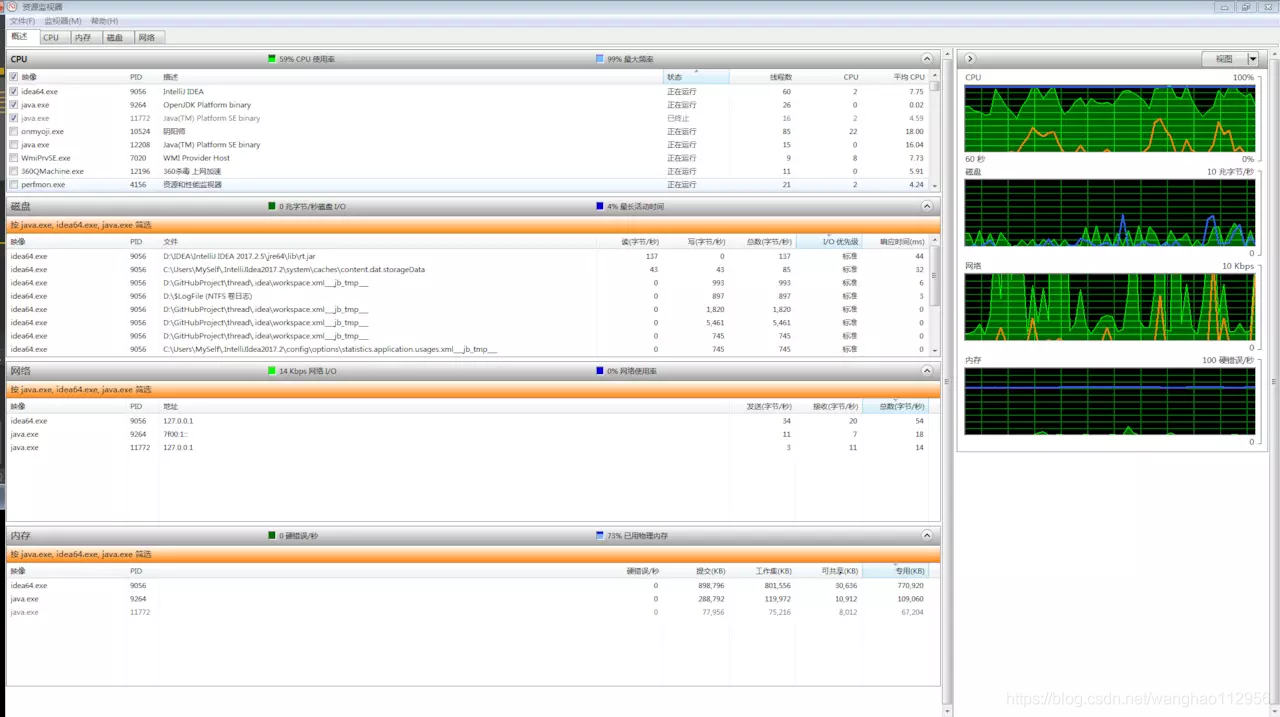 Linux也可以用perf命令查看
Linux也可以用perf命令查看 perf stat -e cpu-clock,task-clock,cs,cache-references,cache-misses java 你的程序名
线程监控
咱们需要把未知的东西变为已知的,黑盒变白盒
你可以尝试用JDK自身的jvisualvm监视
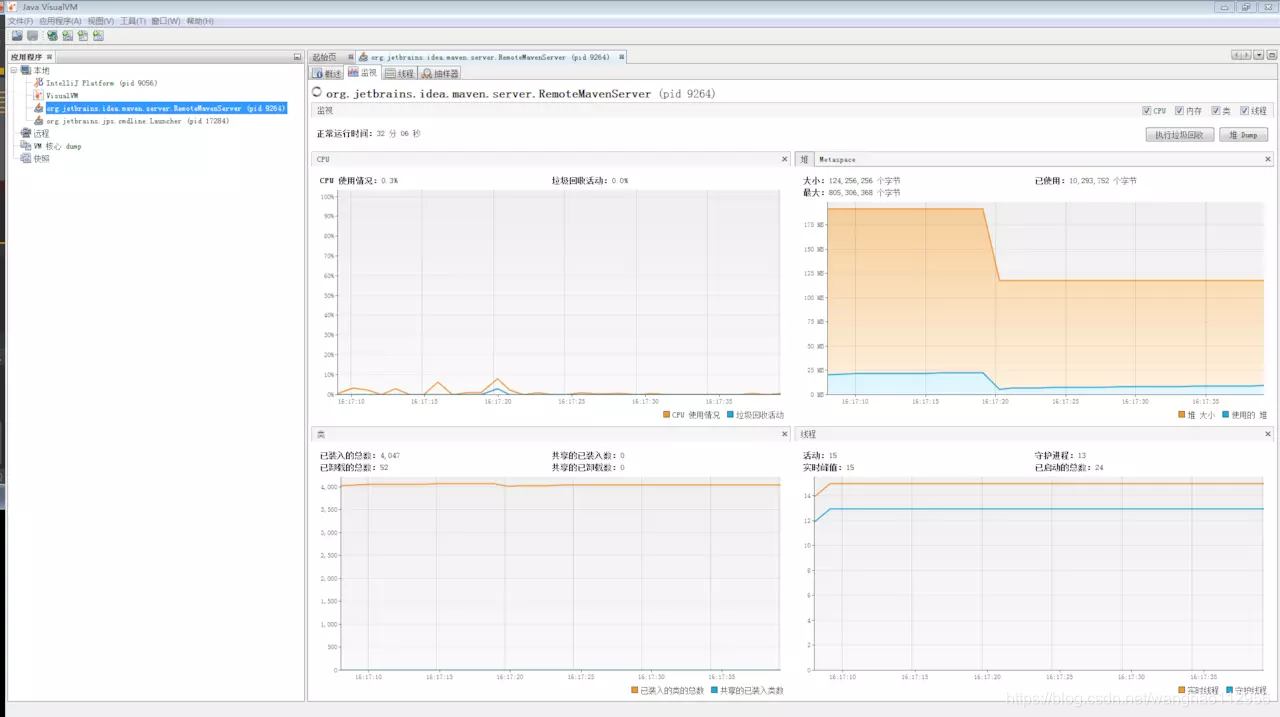
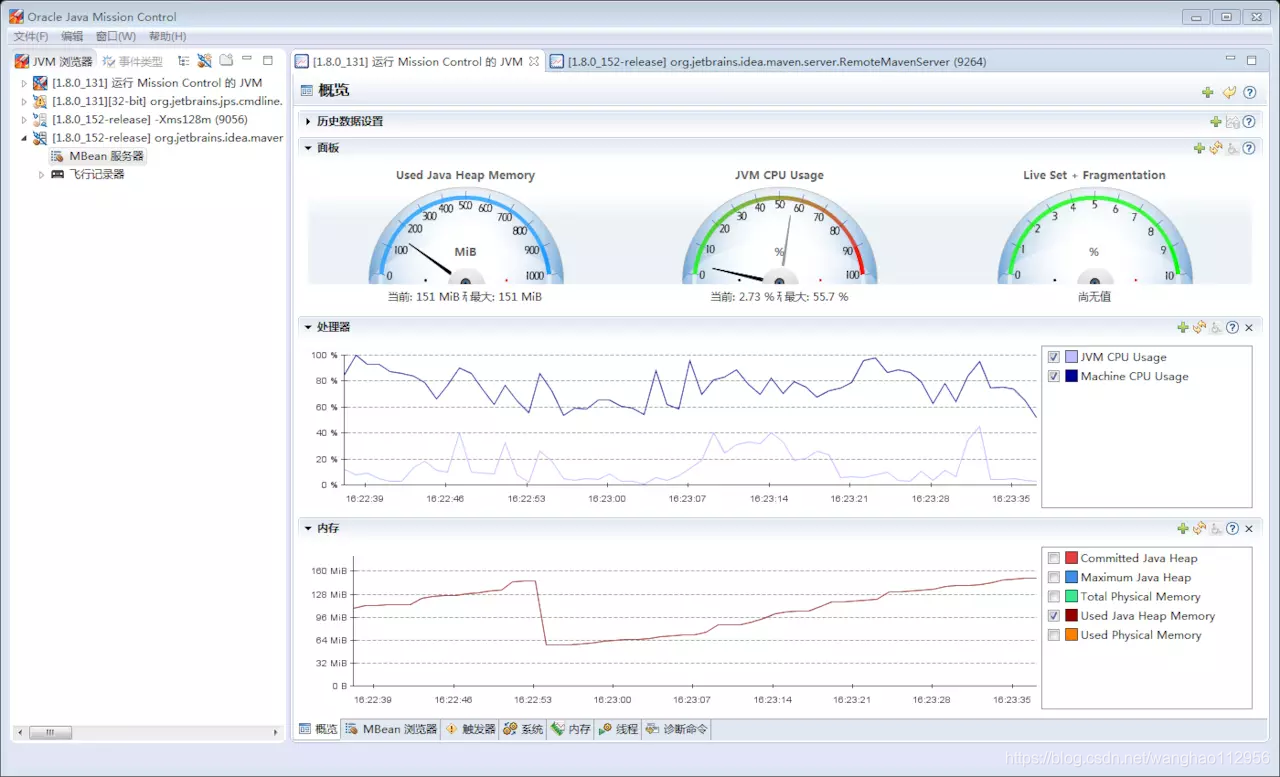
优劣
这个其实大家都基本了解,所以我不打算细讲来着
| 优势 | 劣势 |
|---|---|
| 提供系统的吞吐量 | 线程安全问题 |
| 提高响应性 | 线程的生命特征问题 |
| 充分利用多核CPU | 上下文切换 |
| 最小化系统资源使用 | 可靠性 |
| 简化程序的结构 | / |
关于生命特征,可能就会涉及多种锁
死锁(Dead Lock):即都拥有自己的锁但是又在等对方的锁
T1(L1) 等 L2T2(L2) 等 L1
活锁(Live Lock):一个线程一直尝试某个操作但是无果(就像部分暗恋、舔狗类似····,这个比喻是我和爱人说明后她给我的第一印象)
线程饥饿(Starvation):永远无法获得CPU执行机会,永远处于RUNNABLE状态的READY子状态。
相关术语
| 术语 | 说明 |
|---|---|
| 任务(task) | 任务是线程需要做的,不是一一对应,是一个概念,文件是任务,文件里的多个数据也可以是任务 |
| 并发(Concurrent) | 多个任务在同一时间段内执行,不是顺序执行,是交替执行 |
| 并行(Parallel) | 多个任务在同一时刻执行 |
| 客户端线程(Client Thread) | 有个Hello类,它有自己的方法say(),那么一个main函数,创建它的实体类并调用say方法,那么对于Hello类而言,客户端线程就是main线程 |
| 工作者线程(Worker Thread) | 有个Hello类,它有自己的方法say(),它有自己的一个WorkThread线程,在初始化时,线程就开始start,类似执行自己的日志差不多,那么WorkThread线程就是工作者线程 |
| 上下文切换 | 去看上面的文章内容 :) |
| 显示锁 | Java代码可以控制的锁,包括synchronize和java.util.concurrent.locks.Lock接口的所有类 |
| 线程安全 | 一段操纵共享数据的代码能够保证在同一时间内被多个线程执行而仍然保持其正确性 |
下次再说说,附录的synchronize和volatile。
(想自学习编程的小伙伴请搜索,更多行业相关资讯更有行业相关免费视频教程。完全免费哦!)
转载地址:http://gabp.baihongyu.com/